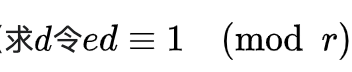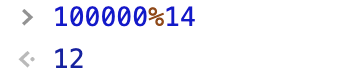加密原理及应用

本文最后更新于：2022年2月12日上午

流程

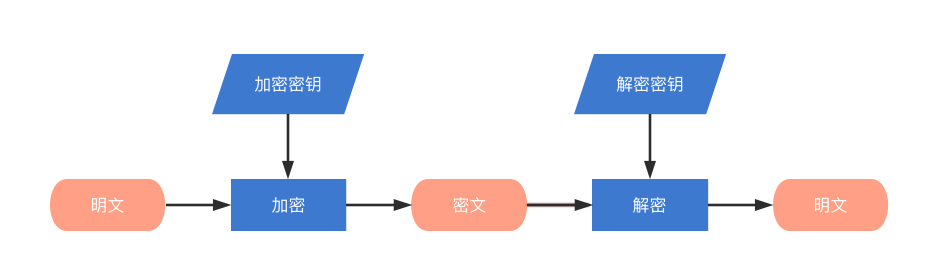
加密

Hash

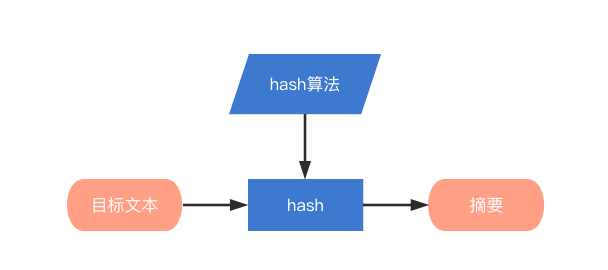
算法

加密

对称加密

DES、3DES-加密标准、3重加密标准

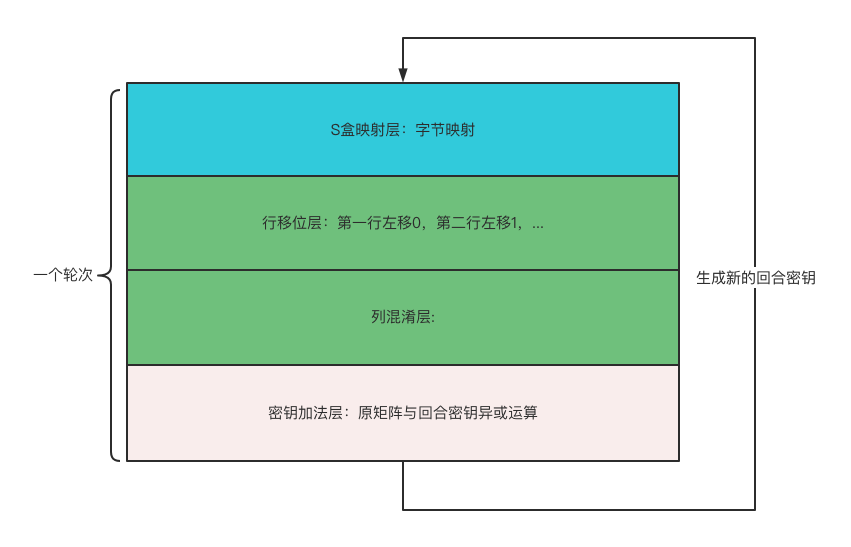
AES-高级加密标准，分组加密在4x4的字节矩阵上运作

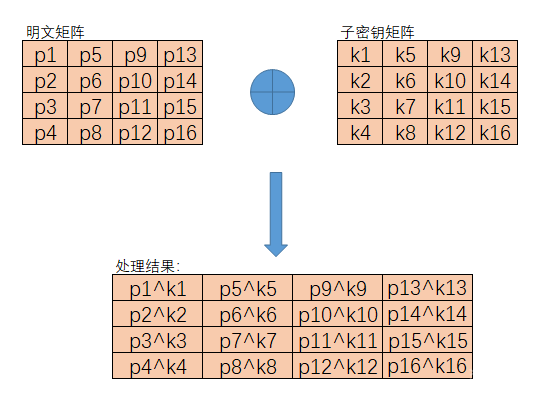
密钥加法层

进行异或运算

字节代换层混淆

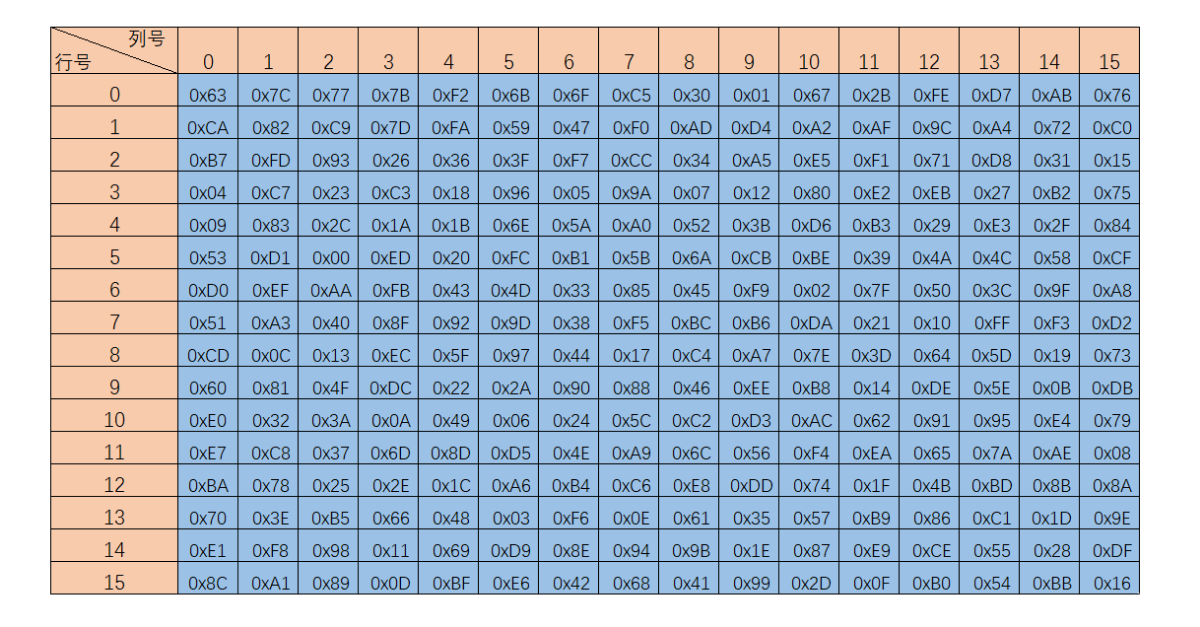
S盒映射：字节到字节的映射

每个字节的高四位作为第一个下标，低四位作为第二个下标

行位移层扩散

对矩阵的每一行进行左移：0123

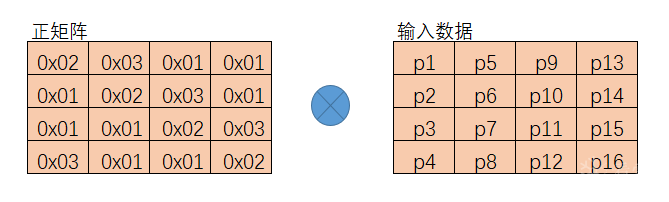
列混淆层扩散

左乘一个矩阵

非对称加密

RSA—公钥加密算法安全性：大整数因式分解的困难性

ECC-椭圆曲线加密算法安全性：解决椭圆曲线离散对数问题的困难性

私钥签名、公钥验证

公钥加密、私钥解密

公钥、私钥的产生（例）

1、素数 p = 2 和 q = 7 ，计算乘积为 N = pq = 14 （小于14与14不互质的数：2，4，6，7，8，10，12，密钥长度2）

2、根据欧拉函数，r = = (p-1)*(q-1) =(2-1)(7-1） = 6

3、选择整数 e = 5，e 和 r 互质，求得 e 关于 r 的模拟元 d

4、即ed-1=xr，d = 11

5、公钥为(N, e)，私钥为(N, d)即公钥(14, 5)，私钥(14, 11)

加密

1、明文为n = 10（需要小于N）

2、密文，即c=12，

解密

1、密文c = 12

2、明文，即n=10,

安全性

1、由公钥、私钥生成第3/4步可知，要求d，需要知道e和r

2、由公钥、私钥生成第2步可知，要求r，需要知道p和q

3、由公钥、私钥生成第2步可知，要求p和q，需要知道N，公钥由e和N组成，所以要破解私钥，需要对N因式分解

结论

密钥长度越长，该算法越安全

已知的攻击方法

1、因数分解

1999 RSA-155（512 bits）被成功分解花费5个月时间 224 CPU hours

2009 RSA-768 (768 bits) 被成功分解

2、时间攻击

利用计算机加密使用的时间推算私钥的内容

总结：明文与密文是一对一的关系

Hash

MD5、SHA

正向快速

给定明文，有限时间、有限资源可以计算出hash值

逆向困难

使用hash值在有限时间内很难推出明文

输入敏感

输入的文本略有不同，摘要需要很大不同

Hash碰撞/散列碰撞

找到hash值一致的两段明文的难度要足够大

总结：输入文本与摘要结果是多对一的关系

使用原则

如果被保护数据仅仅用作比较验证，在以后不需要还原成明文形式，则使用哈希

如果被保护数据在以后需要被还原成明文，则需要使用加密。

应用场景

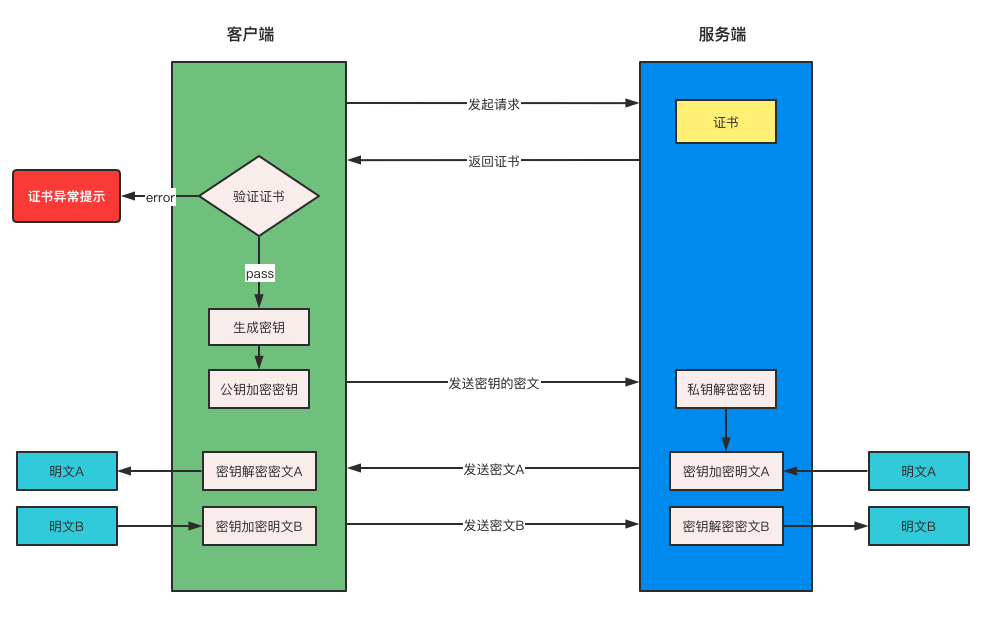
1、HTTPS对数据的加密

对称加密 + 非对称加密

具体方式：

2、Git的无口令访问(SSH)

Hash(MD5) + 非对称加密

具体方式：

Web API的使用

Hash

// 获取crypto对象
const crypto = window.crypto.subtle
const encoder = new TextEncoder()

// 摘要
crypto.digest(
  'SHA-256', // 指定摘要算法
  encoder.encode('Hello World') // 入参ArrayBuffer
).then((digest) => {
   
  const hashArray = Array.from(new Uint8Array(digest)) // 结果ArrayBuffer转换为数组
  // 结果转16进制字符串
  console.log("hash结果:", hashArray.map(b => b.toString(16).padStart(2, '0')).join('')) // 其中padStart用于将字符'0-F'转为'00-0F'，不然摘要长度将发生变化
})

RSA

// 获取crypto对象
const crypto = window.crypto.subtle
const encoder = new TextEncoder()
    
// RSA
// 生成一对公钥、私钥
crypto.generateKey(
  {
    name: "RSASSA-PKCS1-v1_5", // 指定加密算法
    modulusLength: 4096, // 指定密钥长度，至少2048位
    publicExponent: new Uint8Array([1, 0, 1]), // 建议使用65537, [0x01, 0x00, 0x01]，含义：组成公钥的质数
    hash: "SHA-256" // 指定摘要函数名称
  },
  true,
  ["sign", "verify"] // key的用途，指定签名、验证
).then(async (key) => {

  const { privateKey, publicKey } = key // 取公钥、私钥

  // 签名
  const signature = await crypto.sign(
    "RSASSA-PKCS1-v1_5", // 指定签名算法
    privateKey, // 私钥
    encoder.encode(11) // 入参ArrayBuffer
  );
  const hashArray = Array.from(new Uint8Array(signature)) // 结果ArrayBuffer转换为数组
  // 结果转16进制字符串
  console.log("RSA签名:", hashArray.map(b => b.toString(16).padStart(2, '0')).join('')) // 其中padStart用于将字符'0-F'转为'00-0F'，不然摘要长度将发生变化

  // 验证
  const result = await crypto.verify(
    "RSASSA-PKCS1-v1_5", // 指定签名算法
    publicKey, // 公钥
    signature, // 签名
    encoder.encode(11) // 入参ArrayBuffer
  )
  console.log(`RSA验证: ${result}`)
})

AES

// 获取crypto对象
const crypto = window.crypto.subtle
const encoder = new TextEncoder()

// AES
// 生成密钥
crypto.generateKey({
  name: 'AES-GCM',
  length: 256,
}, true, ['encrypt', 'decrypt']).then(async (key) => {

  const iv = window.crypto.getRandomValues(new Uint8Array(12)) // 生成随机数

  // 加密过程
  const Ciphertext = await crypto.encrypt({
    name: 'AES-GCM', // 算法名称
    iv, // 随机数
  }, key, encoder.encode('Hello World'))
  const hashArray = Array.from(new Uint8Array(Ciphertext)) // 结果ArrayBuffer转换为数组
  // 结果转16进制字符串
  console.log("AES密文:", hashArray.map(b => b.toString(16).padStart(2, '0')).join('')) // 其中padStart用于将字符'0-F'转为'00-0F'，不然摘要长度将发生变化

  // 解密过程
  const Plaintext = await crypto.decrypt({
    name: 'AES-GCM',
    iv,
  }, key, Ciphertext)
  // ArrayBuffer转换为字符串
  console.log(`AES明文: ${String.fromCharCode.apply(null, new Uint8Array(Plaintext))}`)
})

第三方库介绍

jsrsasign

优点：

加密方法齐全

Nodejs\web端都可以使用

缺点：

生成密钥耗时长

加密、解密耗时长

jsencrypt

优点：

比jsrsasign加密速度快

Nodejs\web端都可以使用

缺点：

Java验签时不兼容

无法生成rsa密钥

技术

加密

http 下一篇